Исходные данные
Дан файл vector.bin, содержащий 8 чисел двойной точности. Посмотрим внимательно:
$ od -tx1f8 -w8 --endian=little vector.bin
0000000 57 ba 67 e4 bf 2d f3 bf
-1.198669330795061
0000010 fe 60 e6 18 53 47 c2 3f
0.14280165401283534
0000020 32 d9 9b bb 10 57 e0 3f
0.5106280960306206
0000030 2c ca 53 82 93 2a c4 bf
-0.15754932273519395
0000040 9f ba 46 c4 8d 3a f0 bf
-1.014295355514754
0000050 c9 90 f5 b7 0a 23 f3 bf
-1.196055143919738
0000060 e5 d3 cd 56 e0 29 e0 bf
-0.505111856021014
0000070 6b 49 c0 de 63 0d dc 3f
0.4383172679237279
Вычислим длину вектора: \( |\vec{v}| = \sqrt{\sum_{i=1}^n v_i^2 } \) с использованием AVX и SSE инструкций:
Пример “в высоту”
В этом примере используем стек и все xmm регистры — неэстетично, но зато дёшево, надёжно и практично. Используем только SSE.
; simd_h.asm
%define SYS_READ 0
%define SYS_OPEN 2
%define SYS_CLOSE 3
%define SYS_EXIT 60
%define O_RDONLY 0
section .data
vec_outp:
db "v[%lu] = % lf", 10, 0
res_outp:
db "|v| = %lf", 10, 0
path:
db "./vector.bin", 0
byte_size:
db 8
global main
extern printf
section .text
main:
mov rax, SYS_OPEN
mov rdi, path
mov rsi, O_RDONLY
syscall
push rax
sub rsp, 64
read_buffer:
mov rax, SYS_READ
mov rdi, [rsp + 64]
mov rsi, rsp
mov rdx, 64
syscall
close:
mov rax, SYS_CLOSE
mov rdi, [rsp + 64]
syscall
xor r15, r15
xor rdx, rdx
print:
mov rax, r15
div byte [byte_size]
mov rdi, vec_outp
mov rsi, rax
mov rax, 1
movq xmm0, [rsp + r15]
call printf
add r15, 8
cmp r15, 64
jne print
calc:
movsd xmm0, [rsp]
movsd xmm1, [rsp + 8]
movsd xmm2, [rsp + 16]
movsd xmm3, [rsp + 24]
movsd xmm4, [rsp + 32]
movsd xmm5, [rsp + 40]
movsd xmm6, [rsp + 48]
movsd xmm7, [rsp + 56]
mulsd xmm0, xmm0
mulsd xmm1, xmm1
mulsd xmm2, xmm2
mulsd xmm3, xmm3
mulsd xmm4, xmm4
mulsd xmm5, xmm5
mulsd xmm6, xmm6
mulsd xmm7, xmm7
addsd xmm0, xmm1
addsd xmm0, xmm2
addsd xmm0, xmm3
addsd xmm0, xmm4
addsd xmm0, xmm5
addsd xmm0, xmm6
addsd xmm0, xmm7
sqrtsd xmm0, xmm0
mov rdi, res_outp
mov rax, 1
call printf
exit:
xor rdi, rdi
mov rax, SYS_EXIT
syscall
Собираем и запускаем тем же мейкфайлом:
$ make F=simd_h C=1
nasm -f elf64 simd_h.asm -F dwarf
gcc -no-pie -g simd_h.o -o simd
---> running simd_h
v[0] = -1.198669
v[1] = 0.142802
v[2] = 0.510628
v[3] = -0.157549
v[4] = -1.014295
v[5] = -1.196055
v[6] = -0.505112
v[7] = 0.438317
|v| = 2.156239
Работает всё это примерно так:
Пример “в ширину”
Тут уже другой подход - стараемся располагать данные как можно шире. AVX + SSE.
; simd_w.asm
%define SYS_READ 0
%define SYS_OPEN 2
%define SYS_CLOSE 3
%define SYS_EXIT 60
%define O_RDONLY 0
section .data
vec_outp:
db "v[%lu] = % lf", 10, 0
res_outp:
db "|v| = %lf", 10, 0
path:
db "./vector.bin", 0
byte_size:
db 8
section .bss
alignb 32
vector resq 8
global main
extern printf
section .text
main:
mov rax, SYS_OPEN
mov rdi, path
mov rsi, O_RDONLY
syscall
push rax
read_buffer:
mov rax, SYS_READ
mov rdi, [rsp]
mov rsi, vector
mov rdx, 64
syscall
cmp rax, 64
jne exit
close:
mov rax, SYS_CLOSE
mov rdi, [rsp]
syscall
xor r15, r15
xor rdx, rdx
print:
mov rax, r15
div byte [byte_size]
mov rdi, vec_outp
mov rsi, rax
mov rax, 1
movq xmm0, [vector + r15]
call printf
add r15, 8
cmp r15, 64
jne print
calc:
vzeroall
vmovapd ymm0, [vector]
vmovapd ymm1, [vector + 32]
vmulpd ymm0, ymm0, ymm0
vmulpd ymm1, ymm1, ymm1
vhaddpd ymm0, ymm1, ymm0
vxorpd ymm1, ymm1
vmovapd xmm1, xmm0
vextractf128 xmm0, ymm0, 1
vaddpd xmm0, xmm1, xmm0
pxor xmm1, xmm1
haddpd xmm0, xmm0
sqrtsd xmm0, xmm0
mov rdi, res_outp
mov rax, 1
call printf
exit:
xor rdi, rdi
mov rax, SYS_EXIT
syscall
Запускаем так же, результат аналогичный. Но выглядит это теперь вот так:
Смотреть что и как нужно тут и, конечно же, тут. И, самой собой, тут (обязательно соберите себе edb или установите другой отладчик, поддерживающий x64 архитектуру):
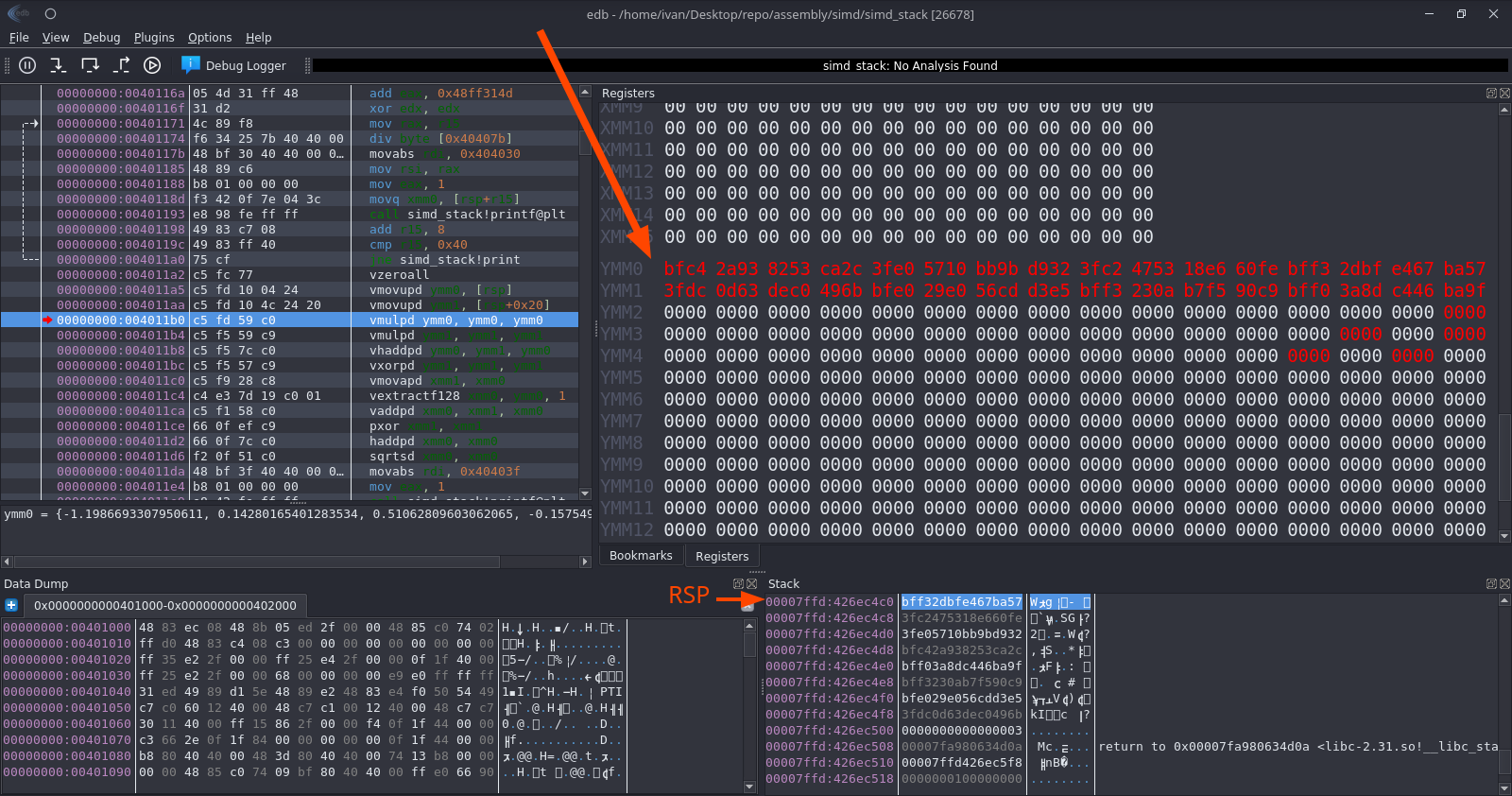
Задание
Вам дан файл, содержащий матрицу \( A_{8 \times 8} \). Вычислить \( N(A) \) с использованием векторных инструкций. Используйте “широкий” подход.
Варианты заданий
Файл. \( N(A) = \max\limits_j \sum_{i=1}^{n} |a_{ij}| \).
Файл. \( N(A) = \sqrt{ \max\limits_i \ |a_{ii}| } \).
Файл. \( N(A) = \sqrt{ \sum_{i=1}^n \sum_{j=1}^m a_{ij}^2 } \).
Файл. \( N(A) = \max\limits_i \sum_{j=1}^{m} a_{ij} \).
Файл. \( N(A) = \sqrt{nm} \max\limits_{i,j} a_{ij} \).
Файл. \( N(A) = \sum_{i=1}^n \sum_{j=1}^m \frac{1}{a_{ij}} \).
Файл. \( N(A) = \sqrt{ \sum_{i=1}^n \sum_{j=1}^m [a_{ij}]^2 } \).
Файл. \( N(A) = \frac{ \min\limits_{ij} |a_{ij}| + 1 }{ \max\limits_{ij} |a_{ij}| + 1 } - 1 \).
Файл. \( N(A) = \sqrt{ \min\limits_{ij} |a_{ij}| } \).
Файл. \( N(A) = \sqrt{ \sum_{i=1}^n |a_{ii}| + |a_{i, n-i}| } \).
Файл.\( N(A) = \frac{ \sqrt{ \sum_{i=1}^n |a_{i1}| + |a_{im}| + \sum_{j=2}^{m-1} |a_{1j}| + |a_{nj}| } }{n + m} \).
Файл. \( N(A) = \frac{1}{nm} \sum_{i=1}^n \sum_{j=1}^m [a_{ij}] \).